הבעיה: מיון מערך בצורה של גלים.
בהינתן מערך של שלמים, המשימה שלנו היא למיין את המערך בצורה של “גלים”, כלומר, שהמערך לאחר מיון יקיים את החוקיות הבאה: a1 >= a2 <= a3 >= a4 <= a5 וכן הלאה..
הערות ודגשים
- סביר להניח שיהיו כמה פלטים אפשריים – במצב כזה אנו נדרשים להחזיר את התשובה הלקסיקוגרפית הראשונה.
תחילה, נפענח את הכתוב, הרמזים ואת הנחות העזר (במידה וקיימות) שיש לנו:
ראשית, נבין מה משמעות השם של המיון:
כמו שגלים מתנהגים בטבע (עולים ויורדים), כך המערך שלנו צריך להיראות, ומשם נגזר השם של המיון.
קלט: מערך שלמים, לדוגמא: [1,2,3]
פלט: עלינו לסדר את איברי המערך על פי החוקיות שהתבקשנו ולהחזיר את התוצאה הלקסיקוגרפית הראשונה.
בדוגמא שלנו, הפלטים הראשוניים האפשריים הם: [2,1,3] ו [3,1,2]. לכן במקרה כזה נחזיר את [2,1,3]
הפתרון
הרעיון: ראשית, נמיין את המערך (מה שיבטיח את הלקסיקוגרפיות בהמשך), ולאחר מכן נרוץ על המערך ונחליף זוגות.
כלומר, בהינתן הקלט [2,1,5,7], ראשית נמיין ונקבל [1,2,5,7]. לאחר שלב החלפת הזוגות נקבל [2,1,7,5] כמצופה.
ובצורה ויזואלית יותר:

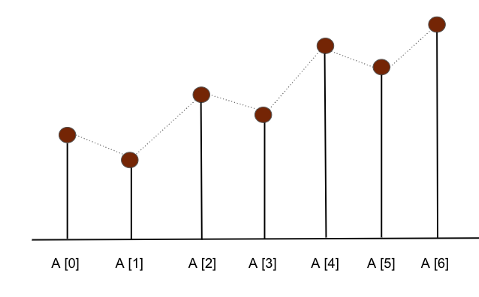
שימו לב שגם ויזואלית ניתן לראות שמדובר בפלט הלקסיקוגרפי הראשון.
גרסת Python:
def wave(A):
A.sort()
for index in range(0,len(A)-1,2):
A[index], A[index+1] = A[index+1], A[index]
return A
גרסת #C:
using System;
class SortWave {
void swap(int[] arr, int a, int b)
{
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
// This function sorts arr[0..n-1] in wave form, i.e.,
// arr[0] >= arr[1] <= arr[2] >= arr[3] <= arr[4]..
void sortInWave(int[] arr, int n)
{
// Sort the input array
Array.Sort(arr);
// Swap adjacent elements
for (int i = 0; i < n - 1; i += 2)
swap(arr, i, i + 1);
}
// Driver method
public static void Main()
{
SortWave ob = new SortWave();
int[] arr = { 10, 90, 49, 2, 1, 5, 23 };
int n = arr.Length;
ob.sortInWave(arr, n);
for (int i = 0; i < n; i++)
Console.Write(arr[i] + " ");
}
}
סיבוכיות:
סיבוכיות זמן ריצה: O(nlogn)
סיבוכיות מקום: O(1)
במקרה זה בחרנו להשתמש במיון מובנה של רשימה (sort) במקום במיון ע”י sorted ובכך חסכנו הקצאת רשימה נוספת.
ענו בעצמכם:
- האם קיים פתרון יעיל יותר בהינתן זה שנוכל להחזיר איזשהי פרמוטציה של הפלט ולאו דווקא את הלקסיקוגרפית הראשונה?
- בהינתן שהתשובה לשאלה הראשונה היא כן, מה יהיה מספר ההשוואות אותן נצטרך לעשות באלגוריתם?
- הפתרון יעבוד במידה וישנם ערכים שווים במערך?
- הפתרון יעבוד במידה והמערך באורך אי זוגי?


